Waterjetting 25d - extending range and cutting power

At the end of the last post I mentioned the benefits that could occur if two jets were directed to intersect at a distance from the nozzle. Marian Mazurkiewicz did a lot of early work on this, and it was written up in an ASTM STP.* Because it has a couple of applications that include potentially extending the range of the jet, this post is somewhat of a short version of parts of that paper. The illustrations are taken from the paper, and the mathematics that is included in the analysis within the paper is not included in this post.

In the initial instant that a flat ended jet hits a flat surface at a shallow angle, two jet flows are formed. A small micro-jet is formed along that surface that moves at a much higher speed in the direction of the arriving jet. A slower jet moves in the opposite direction.

Figure 1. The acceleration of a small segment of an arriving jet on a flat surface (after Mazurkiewicz et al).

By replacing the flat lower surface with a second jet co-axially aligned in the plane of the jets, a similar effect can be achieved, with the second jet moving considerably faster that the arriving jets.

Figure 2. The impact of two jets inclined toward one another at a shallow angle.

For the tests that I described last time, the two jets were inclined toward one another at a relatively small angle (in the range from 1 – 10 degrees) which was partly controlled by the geometry of the cutting head in which they moved.

The improved velocity of the secondary jet can be shown by one of the photographs taken of the impact of two small jets, operated at 60 psi, and intersecting at an angle of ten degrees, using a high speed camera to capture the result.

Figure 3. Intersection of two jets viewed from the top. The jets had broken into droplets at the point of impact, and the shock waves generated by the high speed of the secondary jet formed on impact can be seen around the impact point.

With better quality jets (made from electro-formed nickel built up on a flame-polished mandrel) it was possible to get the jets to intersect while still coherent, and the resulting jets, formed from jets at 10,000 psi, were able to cut thick lenses of pyrite in the field. This was not possible using the 10,000 psi jets alone, without the use of the augmented jets produced by their convergence.

There is a second benefit that can occur where these convergent jets are used in working with harder materials (than coal). It can be illustrated by a photograph of two separate pieces of Berea sandstone into which two different sets of converging jets had been fired.

Figure 4. Two blocks of Berea sandstone each of which had split after having had a pair of convergent jets fired into the top of the block.

The pair of jets converged at the point where the belled-out shape of the cavity transitions to a narrower tapering hole. The larger upper volume is created by the back-flow of the slower moving jet as it cuts back towards the entry hole, reaming out the original passage.

Apart from the evidence of the smaller accelerated jet (through the shape of the cavity) the other interesting point (which was confirmed in a number of tests) is that the restriction of the outflow of water from the cavity, because of the narrowing of the cutting jet paths with depth, and the augmentation of pressure at the impact point, produced enough internal pressure in the blocks to cause them to rupture.

This augmentation was used in Rolla in a number of different applications over the years, although, because of the expense of building the high precision nozzles, these were not used extensively in later work. Rather the jets were formed from two separate flows to nozzles on the end of two short lengths of hose. These jets could then be adjusted to change the intersection angle of the jets, which was also adjusted through raising and lowering the head, so that the intersection point fell below the surface of the target. This meant that the jets had to penetrate a little into the rock by themselves, before they intersected and generated the higher pressure small penetrating jet and concomitant increase in local pressure of that jet.

Figure 5. Different approaches to the use of converging jets on a rock surface. That on the left is the MS&T version, that on the right was carried out at the University of New South Wales**.

The MS&T approach was based on the work we had carried out in the field, where the jets were to converge on the surface of the target, so that the jet would be able to penetrate through rock materials that it would not normally be able to cut. In the trials in the mine an intersection angle of 2 degrees was found to be best.

The Australian approach followed on Frank Roxborough’s ideas of trying to generate larger chips when cutting into rock, in order to lower the energy required for material removal.

The Australian team however, found it more useful to converge the jets, closer to the nozzle which was less tightly manufactured, and focused the streams within the rock body. In this way the stresses set up within the rock were found to invariably produce large single chips of rock roughly conical in shape with an angle similar to that of the impacting jets. Interestingly it was reported that there was little evidence of jet cutting action in these tests where a jet at a pressure of 40,000 psi was cutting into a 30,000 psi uniaxial compressive strength basalt – something normally impractical even at those jet pressures. The results also were reported to show that the specific energy required for this technique was one to three orders of magnitude less than for conventional cutting of slots by jet action. Subsequent traversing tests on the rock were preliminarily reported to substantiate the results from the static testing.

* Mazurkiewicz, M., Barker, C.R., Summers, D.A., "Adaptation of Jet Accumulation Techniques for Enhanced Rock Cutting," in Erosion: Prevention and Useful Application, ASTM STP 664, W.F. Adler, ed, ASTM, 1979, pp. 473 - 492.
** Lin, B., Hagan, P.C., Roxborough, F.F., "Massive Breakage of Rock by High Pressure Water jets," 10th International Symposium on Jet Cutting Technology, Amsterdam, Holland ,October, 1990, pp. 399 - 412.

Waterjetting 25c - more thoughts on jet range

A single waterjet, whether with or without abrasive, will cut a tapering slot as it penetrates into a target material. This is because, as the jet penetrates into the surface, the outer edges of the jet lose their energy in cutting, and the narrower central core remains capable of cutting, on a continually narrowing path, as the cut deepens.

Figure 1 Tapered cut made with a single jet traverse in contrast with the wider cut made with two diverging jets.

While the above statement is generally true, it is not completely so, since if the speed of traverse of the jet is reduced, then the continued addition of further water along the cut plane will be sufficient for the outer layers of the jet to be able to continue to cut and this may reach the point that there is no taper along the edges of the slot, or it may even taper inwards. For an abrasive jet cutting into titanium, that transition occurs at around 0.2 inches/minute, depending on jet parameters. (Note that this is less related to the target thickness, although it is controlled by the cuttability of that material, and that the critical speeds for cutting with water along are at least one and often two orders of magnitude greater).

Figure 2. Plot of taper angle with traverse speed.

Unfortunately the speed at which the edge is cut perpendicular to the top surface of the target is usually too slow to be economic, and, in consequence, the normal process is to slightly tilt the cutting head into the edge with the desired surface, and making the opposing surface carry an exaggerated tilt. This then allows a faster cut, again with the optimal speed being a function of both tilt angle and jet parameters.

When the objective, however, is to achieve a deeper cut, particularly where multiple passes are concerned, and head movement into the cut is allowed, then a different strategy can be followed.

Back when we were developing the longwall mining machine we called Hydrominer, we used a dual-jet system, because, when cutting coal, the material between two adjacent, concurrent cuts is removed as those cuts are made. Thus the jets, in a second pass, do not make contact with the walls of the cut until reaching the back of the previous cut. (The second image in Figure 1).

Figure 3. Slot cut by the Hydrominer, looking down, and with the slot through which the jets cut out from the head visible on the left edge of the machine.

However, in harder materials, including rock with some degree of cohesion, it is possible to run two jets almost side by side, and leave a rib of material between the cuts, so that jet attenuation in dual cutting is still a problem if the jets are parallel.

Again the answer is to tilt the jets, although if small jets are used, multiple jets may lose in overall range, because of the reduced diameter of the individual streams.

In this case it can be more effective to combine the jet flows into a single jet, but to either orbit or rotate this slightly off-axis so that the jet is cutting a slightly wider track along the path, and with a widening slot with depth, so that, again, subsequent passes, where the nozzle moves into the slot, do not encounter the walls of the cut until the back of the previous cut.

Back in the days when we were first testing the coal mining machine, we were mining coal in northern Missouri, and the coal had a large number of pyrite lenses in it. These lenses could be up to four inches thick, and, while the coal was friable and easy to cut, the pyrite lenses were much harder and dense. They could not be easily cut with the jets, which were operating at 10,000 psi, and the machine was not performing very well.

There were two ways in which we overcame the problem. The first was to adjust the two jets that were cutting the slot into which the cutting head was moving. As I mentioned earlier with a slight divergence angle between the jets, the slot was cut wide enough (around 2-inches) for the leading edge of the head to enter the cut, and the depth (around 9-inches) was enough to give leverage for the head to peel the rib of coal from the solid.

Figure 4. Comparison of results in the field with initial lab-designed nozzle.

When we encountered the pyrite, we changed the angle of the jets, so that instead of diverging the converged at varying distances in front of the head. When the two jets come together at this shallow angle (as with shaped charge formation) they form a very high speed jet, as well as a slower moving wider stream.

When this combination replaced the diverging jets on the head, this higher-speed jet was sufficiently powerful that it cut through the pyrite, and gave a free surface for the rest of the lens to break into. (Depths of cut up to 3-ft were achieved, although the slot was less than one-inch wide). This worked well for the side of the slab that was now liberated, since the jet had broken it free, and the head could move it away from the face, and into the conveyor track.

The only problem that we had at the time, was that the convergent jet was formed in the center of the slot being cut and in the center of the leading edge of the mining head. The slot was no longer wide enough for the head to enter (the converging jet gave a slot about half-an-inch wide IIRC). As a result the pyrite on the solid side of the cut now engaged with the leading edge of the head and stopped progress.

The answer to the problem, which we arrived at over time, was to change the angle of the axis of convergence of the jets, so that, instead of being in the center of the slot, the convergent jet was inclined over towards the solid, and cut into the pyrite just ahead of the outer edge of the mining head. In this way, since the material to the free side of the head was being moved out of the way by the advance of the machine, the jets still cut clearance for the head to move forward. At the time we were only able to get the machine up to a speed of 10-feet a minute, but by taking a bite of 36-inches at a time, we were able to match the productivity of existing mining machines of the period. (The coal seam was 5-ft high). The guard design on the head was also changed to give a sharper edge on the solid side of the machine.

Figure 5. Change in head guards to penetrate pyrite.

Very little work has been carried out on convergent jet systems since that time, which is a pity since it allowed us to mine harder material than the main jet pressure available was allowing us to achieve.

Waterjetting 25b - range with abrasive

In the last post I wrote about the impact of smaller jet diameters, and higher pressures, in truncating the range over which a waterjet is effective. The same is true, to an extent, when one adds abrasive to the water.

Our “green tube” test has been described in earlier posts, where the distance over which particles settle out of the jet provide a measure of how much energy they were given. However it is not that simple to interpret the results from these tests. The reason is that, as with a plain waterjet, the range of the particles is controlled to a degree by the size of the individual grain. Why is this? Well this series tries to keep formulae to a minimum, but one is needed in the answer to that question.

The origin comes from our friend Newton, whose Laws have come down to us over the centuries, and the second of which states:

Force = mass x acceleration

Consider that when an initially stationary particle is sitting in a jet stream, the force being applied to it by that jet is equal to the pressure of the jet, multiplied by the area over which the pressure is applied. If for simplicity we assume that the particle is spherical, then the area over which the pressure is applied (assuming that the particle is centralized within the jet stream) is equal to the pressure multiplied by the cross-sectional area, which is given by the product of the square of the radius multiplied by pi.

On the other hand the mass of the particle is related to the volume, which is in a cubic relationship with the radius. Thus if these two terms are substituted in the equation above, and combining all the non-radial terms into a constant results in an equation where:

Acceleration x radius cubed x constant = pressure x radius squared x constant

Rewriting this gives:

Acceleration = (1/radius) x pressure x constant.

This means that larger particles have smaller accelerations for a given pressure, while smaller ones accelerate faster.

However, and this pertains to the results we saw from the green tube tests, just as the smaller particles are accelerated faster while in the jet stream as it passes through the nozzle assembly, so those smaller particles will decelerate faster when having to travel through the relatively stationary air outside of the nozzle.

Thus if you are, for example, using a smaller jet flow (and smaller jet orifice in consequence) then the normal practice is also to reduce the size of the focusing tube, and – to otherwise keep the system practical – to also reduce the size of the abrasive particles fed into the system.

However, while this gives a better cutting effect immediately under the nozzle (hence the widespread recommendation to restrict the standoff distance between the nozzle and the target to about a quarter-of-an-inch) there is a more rapid decline in the speed of the particles as they move away from the nozzle. The net result is a shorter range for the jet, and a shorter cutting depth in consequence.

There is a small caveat to holding this as an absolute conclusion. Back in the days of the U.S. Bureau of Mines Dr. George Savanick showed that where an abrasive jet could be held within a relatively narrow slot, as it cut down, that the walls of the slot tended to concentrate the jet, and thus extend its range beyond that achieved if the jet were, for the sake of example, just cutting through a piece. Thus, when not through-cutting the part, there will be some extension of the jet range, and this has to be considered when setting the operating parameters for a particular job.

Which brings us back to defining the optimum size of the operating plant required to complete a given job, and a resolution of the optimum parameters for carrying out the job.

As I have noted before, this is not a simple and straightforward choice. Proponents of different operating systems will advocate different solutions based on the units that they are most familiar with. And there are arguments that can be made for different choices. However, in making the choice of the best system to use, one must be aware of the limitations (as well as the benefits) of the different choices that might be available.

Consider that a lower pressure, higher flow rate system might use larger particles, and thus be able to cut through a target plate of a given thickness with better speed than a higher-pressure, lower flow rate alternative. However were the target to be of a thinner stock where the range of the jet is not that critical, then the higher pressure system may well give the better performance (given, inter alia, that it will also use less abrasive and water).

Making a selection as to the better operating system, therefore, requires a clear understanding of the different modes in which the system is likely to be used. Will it be for relatively thin materials, where high precision and narrow cuts are required, but the material need not necessarily be through-cut. Or is the system one where a cut may be required through perhaps 30-inches of reinforced concrete in a reactor (of which more in a later post). In the latter case the lower pressure, higher flow rate jet, with the ability to use larger particles and sustain their velocity further, when further confined by the walls of the cut. The former condition would argue for the use of a higher-pressure, lower-flowrate combination, while the latter (as a generalized statement) would incline more to the lower pressure alternative. (And the terms are relative, since in the latter case we are likely still talking about pressures of around 30,000 psi or higher to achieve the depths of cut within the reinforced concrete.)

Much is written about having to make absolute choices in cutting, but in many cases it is only a matter of relative performance, with systems across a range of parameters being able to effectively achieve the goal. The selection of which system to use should focus more on the normal range of materials that one is expected to cut in the normal course of operations. (And slicing though parts of a nuclear reactor is not normal in most aspects of this business).

Iceland livens up

Jón Frímann points to an interesting pattern of earthquakes around the caldera at Bardarbunga, suggesting that the volcano might be getting ready to erupt.

Icelandic Met Office.

It is hard to tell from the webcams, since Bardarbunga 2 is shaking too much. This may be bad weather - except that the weather shown at the first camera shows that it is clear on the left, suggesting that there is a lot more ash being thrown into the air. So this may be a more significant eruption already, due to the ash cloud.

Bardarbunga web cam at 10:43 am 12th Sept.

UPDATE: The increasing concern comes from the clouds of SO2 that are being emitted from the craters. This poses threats, not only to those in Iceland, but also potentially to some in Northern Europe. The smell of sulphur is now being detected in Norway. The latest path for the gases has been posted:

Figure 3. Path of the gas cloud from Iceland.(RUV )

The Icelandic Met Office is now issuing bulletins in English as well as Icelandic.

More later.

Waterjetting 25a - choosing jet parameters for range.

The range over which a waterjet is able to cut material can widely quite significantly, depending on a wide range of factors, including abrasive content. An earlier post described the way in which students in a waterjet class were shown some of the difficulties in assessing risks arising from the use of a waterjet, and the range over which it was dangerous. Simplistically the students first cut along a plywood panel to see how far from the nozzle the jet would remove wood.

Figure 1. By slightly tilting the 4-ft wide panel and then having students move the jet past the board along the left-hand edge, a measure of the range of the jet could be obtained.

However, after the students had decided that, for the 10,000 psi 0.03-inch diameter jet, the cutting range was about ¾ of the way across the width (i.e. 3 ft) they were then tasked to pass the jet, as fast as they could, over a piece of pork that was at least a foot further away from where they estimated the distance that the jet stopped cutting.

Figure 2. A piece of pork after being “sliced” by a 10,000 psi waterjet.

The pork was typically cut to a depth of over an inch, grooving into the bone at a distance that the student had previously decided was “safe.” It was pointed out to the class that the pork was a good simulator for human flesh.

The point of the demonstration was fairly obvious, but it does highlight that the distance at which a jet stops cutting one material because of insufficient energy, may still be quite a distance closer than that critical distance for other softer materials.

In one of the earlier scientific papers on waterjet cutting Leach and Walker plotted the drop in jet pressure from two different nozzle shapes, against the distance from the nozzle.

Figure 3. Decline in jet pressure with distance from the nozzle (Leach and Walker)

With poorer nozzle designs and in cutting many harder materials the critical distance at which the jet pressure falls below half the original pressure, and thus in many materials stops cutting, is at around 125 nozzle diameters. For a 0.03-inch diameter jet, cutting a distance of 36 inches takes the range to 1,200 diameters. And while that range is partly because we have significantly improved the fluid flow into the nozzle it relates, as noted, also to the strength of the material being cut.

One reason to mention this is that I have seen, both in photos and real life, people foolish enough to hold their hands in front of a 40,000 psi waterjet, as an illustration of the safety of the tool at even a short range. (Typically they were using jets of around 0.006 inches diameter with the hand about a foot from the nozzle). A slight increase in nozzle diameter, undetected by the operator, or a change in fluid content (such as by adding a long-chain polymer (such as Superwater) could extend the range of the jet several-fold, so that the unsuspecting operator might lose several fingers before realizing the change in conditions.

An earlier post described the work of Clark Barker and Bruce Selberg, who demonstrated that an increase in polish of the inner surfaces and a smooth transition path into the orifice could extend the cutting range of a jet in harder materials from 125 diameters to over 2,000.

Achieving a smooth flow path to the orifice is critical to superior performance, though – as I have mentioned before – it was at one time surprising to me how many contractors did not even have the nozzle insert mating with the end of the supply pipe. Rather, with the nozzle insert held in a holder, they just turned the latter until it was tight, not always achieving contact between the back of the nozzle insert and the pipe. In addition there have been many cases I have seen where the nozzle insert inlet diameter differs from that of the internal diameter of the connecting pipe Again this will interfere with performance away from the nozzle.

Assuming, however, that one has stabilized the flow into the nozzle, and that it is of the right shape, how can one increase the jet throw distance further? The obvious, and wrong, answer is to up the pressure that is driving the jet.

Why is this the wrong answer? Well, if one considers what happens when a jet shoots out into the air, as one can see in a high-speed flash photograph:

Figure 4. Flash photograph (exposure at about one-millionth of a second) of a high speed waterjet showing the structure.

As the jet travels through the air, so the relatively stationary air around the jet strips off, and decelerates, the jet in layers starting from the outside. These show up as backward pointing stringers flowing out from the main jet stream. As the outer layers are peeled off (as with stripping the layers from an onion) so the remaining diameter gets less until, as in the picture above, there is no jet left.

Consider that with a higher driving pressure that there is a greater differential between the air speed and that of the jet, and obviously the stripping action will occur more rapidly, reducing the overall range of the jet.

Now consider if, instead of putting that additional power into pressure/jet velocity one were, instead to put it into additional flow. Then there are more layers of the jet to strip away, and the differential is not as great. As a result, when one compares the performance of two jets one gets:

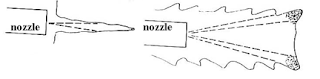
Figure 5. Comparing the performance of two jets.

Notice in this case that relatively close to the nozzle the two jets, cut to roughly the same depth, and in this range the higher pressure, smaller jet has advantages in that the thrust it applies to the holding tool is less, and the total amount of water used is also less (roughly 4.3 gpm rather than 7.3 gpm). However if one is cutting at a greater standoff distance between the wall and the target, then at about 4 ft from the nozzle (1000 diameters of the larger, 1500 diameters of the smaller) the lower pressured, higher flow rate jet becomes more effective.

This relative change in nozzle effectiveness with pressure and diameter was also reported from results at lower pressure when developing nozles for cutting coal in Germany.

Figure 6. Comparing the pressure profiles of jets at two different diameters and pressures, as a function of distance from the nozzle.(Benedum et al)

Note that here, again, at about 8 m from the nozzles, both jets are producing about the same impact pressure, while closer to the nozzle the smaller (blue line) jet has a better profile (at 0.78 inch diameter, and 1,300 psi) than the larger (black line) jet (at 1-inch diameter, and 1,000 psi). But at greater distances the lower pressure, larger diameter jet becomes more effective.

There is, in short, significant benefit to determining, before one starts, what the objective is and over what range the jet is expected to cut, since both will help decide what set of jet operating conditions will give the better result.

References Leach, S.J., and Walker, G.L., "Some Aspects of Rock Cutting by High Speed Water Jets," Phil. Trans. Royal Society, London, Vol. 260A, pp. 295 - 308.
Barker, C.R. and Selberg, B.P., "Water Jet Nozzle Performance Tests", paper A1, 4th International Symposium on Jet Cutting Technology, Canterbury, UK, April, 1978.
Benedum, W., Harzer, H., and Maurer, H., "The Development and Performance of two Hydromechanical Large Scale workings in the West German Coal Mining Industry," paper J2, Proc. 2nd Int. Symp. Jet Cutting Tech., BHRA.